Binary Tree Vs Search Binary Tree

   Last Updated: 06 October, 2024       🕓  6 Mins Read

Binary Trees and Binary Search Trees are tree-based data structure in computer science that organizes data hierarchically. Both are used for different purposes and have distinct properties. In the tutorial, we are going to explore about difference between both. We will begin by defining each structure and then highlight their key differences.

What is a Binary Tree?

A Binary Tree is a fundamental data structure in computer science that organizes data hierarchically. In Binary tree, each node can have maximum two child nodes, referred to as the left child and the right child. The topmost node is called the root and the bottom-most nodes are called leaves.

Binary trees are widely used due to their simplicity and efficiency in various applications such as data storage and retrieval, expression evaluation, network routing etc. and can also be used to implement various algorithms such as searching, sorting, and graph algorithms.

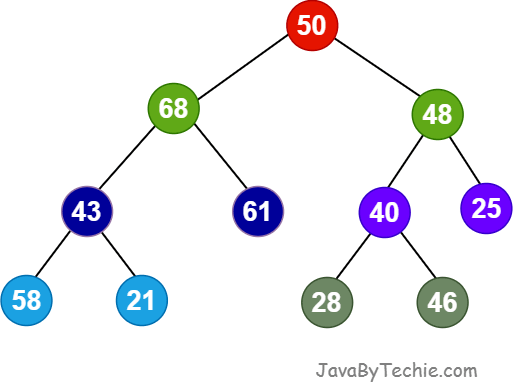
In a Binary Tree, every node has three parts:

1. Data
2. Reference of left child node
3. Reference of right child node

What is Binary Search Tree?

A Binary Search Tree (BST) is a special type of data structure that organizes data in a tree-like structure. It has a single starting node called the root, and each node can have at most two child nodes: a left child and a right child.

In BST, the value of each node is greater than all the values in its left subtree and less than all the values in its right subtree. This ordering property makes BSTs efficient for searching, inserting, and deleting elements.

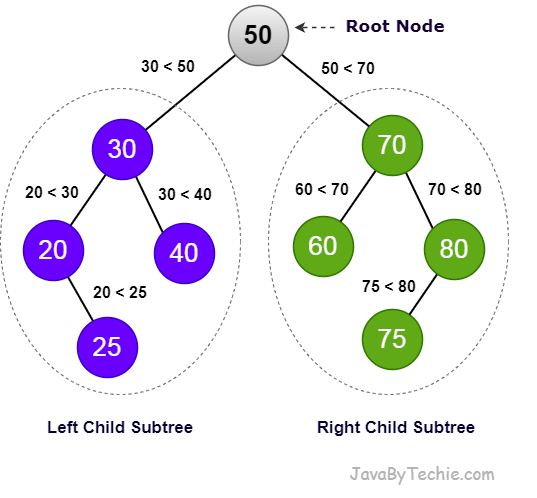
In the tree above, 50 is the Root node and it has two child nodes 30 (create left subtree) and 70 (create right subtree).

Important points of Binary Search Tree (BST):

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• The left and right subtrees must be binary search tree (BST).
• Duplicate nodes are not allowed (but BST may have duplicate values handled differently).

Difference between Binary Tree and Binary Search Tree

Feature	Binary Tree	Binary Search Tree
Defination	It is a non-linear data structure in which each node has less than or equal to two children, and each of the left and right subtrees should also be a binary tree.	It is a non-linear data structure in which each node has less than or equal to two children, and each of the left and right subtrees should also be a binary search tree.
Node Ordering	No specific order required for child nodes.	Left subtree contains nodes with keys less than the parent's key. Right subtree contains nodes with keys greater than the parent's key.
Search Efficiency	Search can be inefficient, especially in unbalanced trees (O(n) in the worst case).	Search is generally efficient, with an average time complexity of O(log n) for balanced BSTs.
Insertion/Deletion	Insertion and deletion can be more complex and may not guarantee balanced structure.	Insertion and deletion operations maintain the BST property, ensuring efficient search performance.
Balancing	Not inherently balanced. May require additional mechanisms to maintain balance.	Some BST variants (like AVL trees, red-black trees) have built-in mechanisms to maintain balance and ensure logarithmic time complexity for all operations.
Use Case	General-purpose hierarchical data.	Efficient searching, insertion, and deletion.

In Summary:

Binary Tree: A general-purpose tree structure with no specific ordering constraints.

Binary Search Tree: A specialized type of binary tree with an order property that allows for efficient search, insertion, and deletion operations.

While both are tree-based data structures, binary search trees offer significant advantages in terms of search efficiency and are widely used in various applications where fast lookups are essential.