Types of Graph in Data Structure

   Last Updated: 20 January, 2025       🕓  5 Mins

Types of Graph in Data Structure:

1. Finite Graph: If the graph G=(V, E) has a limited number of vertices and edges, it is referred to as a finite graph.

   

2. Infinite Graph: The graph G=(V, E) is called a finite graph if the number of vertices and edges in the graph is interminable.

   

3. Trivial Graph: If a graph G = (V, E) contains only one vertex and no edges, it is called a trivial graph.

   

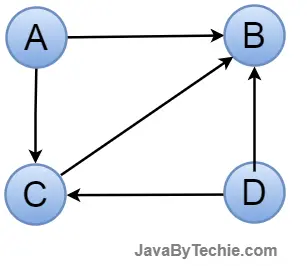
4. Directed Graph: A graph that has a set of nodes connected by edges, each with a direction, is called a directed graph. A directed graph, also referred to as a digraph.

   

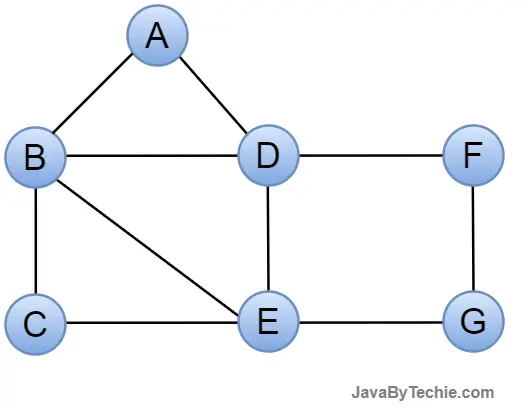
5. Undirected Graph: An undirected graph consists of nodes and links that connect them. The order of the two connected vertices is irrelevant and without direction. We can create an undirected graph with a finite number of vertices and edges.

   

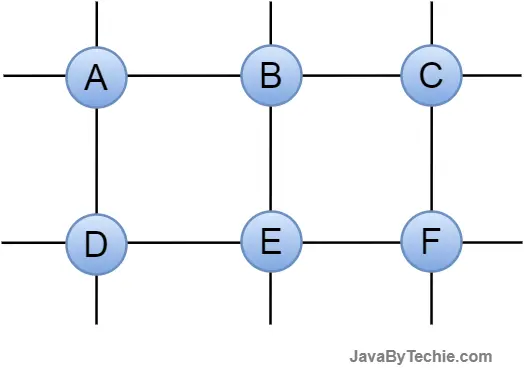
6. Weighted Graph: In a graph, if each edge has some value or weight, it is called a labeled or weighted graph. The value or weight represents the cost of traversing that edge.

   

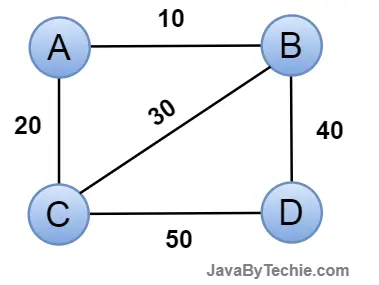
7. Cyclic Graph: A cyclic graph is a type of graph in which at least one path leads back to the same vertex, creating a cycle. Such a type of graph is called a cyclic graph.

   

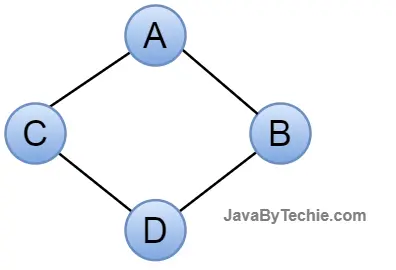
8. Acyclic Graph: Acyclic graphs are those that do not contain any cycles.

   

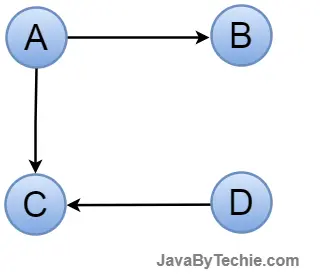
9. Directed Acyclic Graph: A directed acyclic graph (DAG) is one that contains directed edges but no cycle. It uses an ordered pair of vertices to represent the edges since it directs them and holds certain data.

   

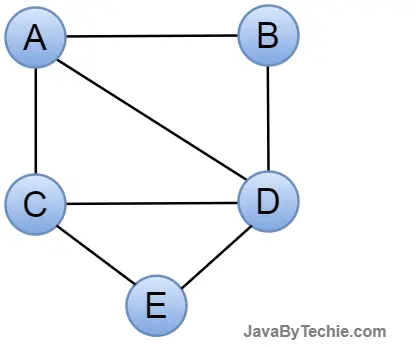
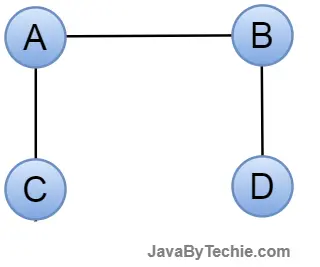
10. Simple Graph: A simple graph is one in which each pair of nodes or vertices has only one edge. As a result, only one edge connects two vertices, representing one-on-one interactions between two constituents.

    

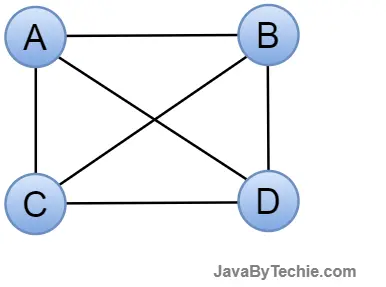
11. Multi Graph: A graph G= (V, E) is called a multigraph if there are many edges connecting two vertices. A Multigraph does not contain self-loops.

    

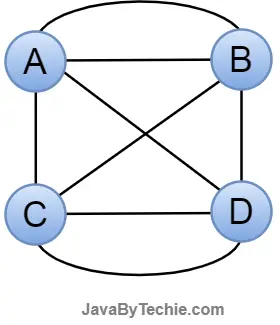
12. Connected Graph: A graph is said to be linked if there is a path connecting any two of its vertices.

    

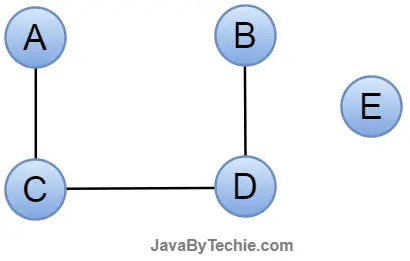
13. Disconnected Graph: A disconnected graph is a type of graph in which there are at least two vertices that are not connected by a path. This means that the graph can be divided into two or more components, each of which is connected internally but not to the other components.

    

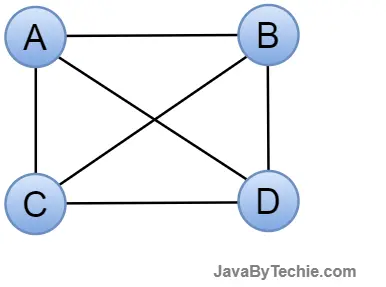
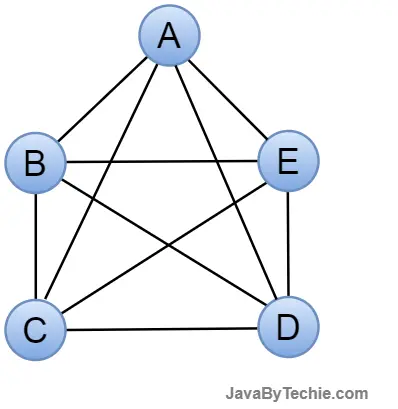
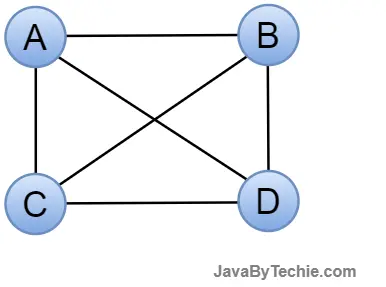
14. Complete Graph: A complete graph is another type of graph in data structure; in this graph, every pair of distinct vertices is connected by a unique edge. A complete graph is an undirected graph, and it is also known as a full graph because each vertex's degree must be n-1.

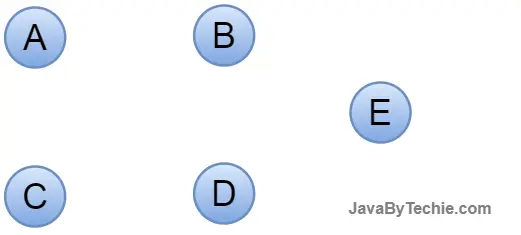
15. Null Graph: A graph that has multiple vertices but no edges connecting them is known as a null graph. A null graph is a revised version of a simple graph.

    

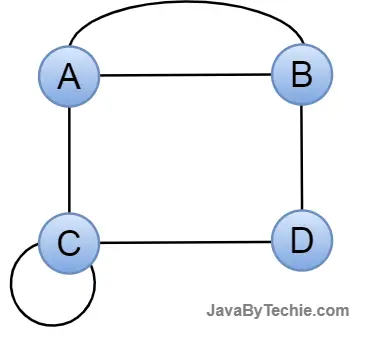
16. Pseudo Graph: If a graph contains a self-loop besides other edges, it is a pseudograph.

    

17. Regular Graph: A regular graph is one that has the same degree at each vertex. As a result, the entire graph is a regular graph.

    

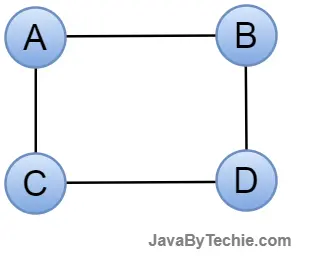
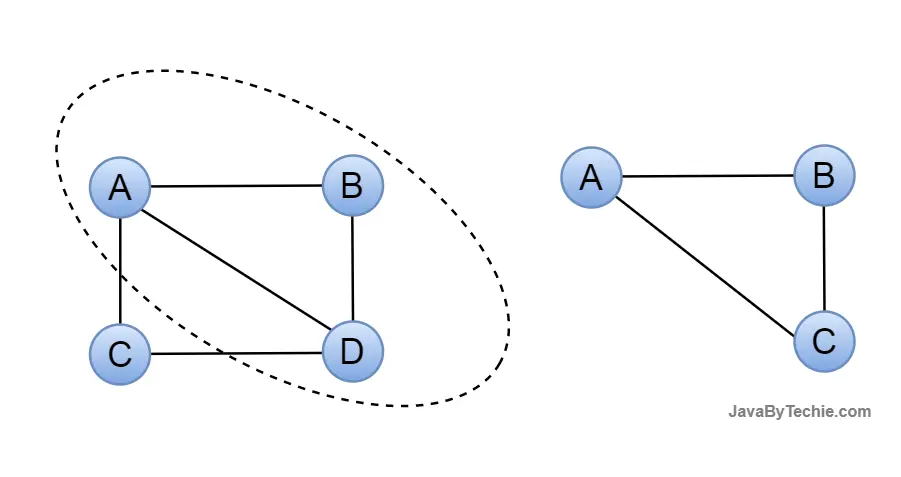
18. Subgraph: A subgraph is a set of vertices and edges from one graph that are subsets of another graph.