

Last Updated: 06 October, 2024 5 Mins
DFS (Depth-First Search) and BFS (Breadth-First Search) are Graph traversal algorithms are used to exploring and searching graphs and trees. Both are used for the same purpose but they follow the different approach to traveral.
Before we look into the basic difference between BFS and DFS, let's briefly understand about BFS and DFS.
Breadth First Search (BFS) is a graph traversal algorithm. BFS first traverse all the neighboring nodes of the starting node once all neighboring nodes are visited, then it will move on to the next level as given in the image below.
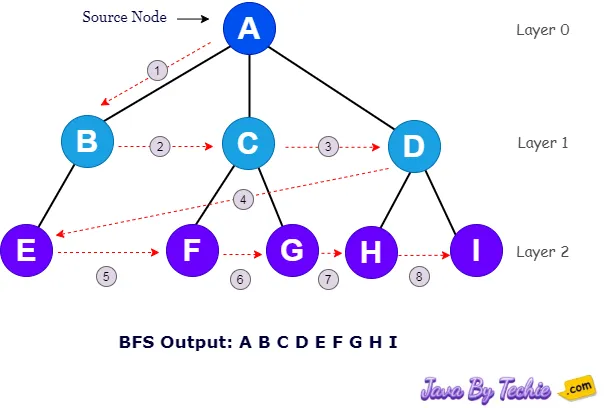
BFS traversal of a graph produces a spanning tree as final result. Spanning Tree is a graph without loops.
BFS is the foundation of numerous well-known graph algorithms, including Prim's algorithm, Dijkstra's shortest path, and Kahn's algorithm.
Depth-First Search (DFS) is a graph traversal algorithm that explores as far as possible along each branch before backtracking. It starts at a root node and explores its neighbors one by one, going deeper into the graph until it hits a dead end or a previously visited node. Then, it backtracks to the last node with unexplored neighbors and continues the process.
| Characteristic | BFS (Breadth First Search) | DFS (Depth First Search) |
|---|---|---|
| Data structure | BFS uses Queue for finding the shortest path. | DFS uses a Stack to find the shortest path. |
| Time Complexity | O(V + E) (V = vertices, E = edges) | O(V + E) (V = vertices, E = edges) |
| Space Complexity | O(V) (due to queue storing nodes at the current level) | O(V) (due to recursion or explicit stack) |
| Speed | BFS is slower than DFS. | DFS is faster than BFS. |
| Memory uses | BFS requires more memory space. | DFS requires less memory space. |
| Traversal approach | Explores all neighbors at the current level before moving to the next level. | Explores as deep as possible along one branch before backtracking. |
| Cycle Detection | Can detect cycles, but less commonly used for it. | Useful for detecting cycles in directed or undirected graphs. |
| Graph Representation | Can be used with both adjacency lists and matrices. | Can be used with both adjacency lists and matrices. |
| Tree Traversal | Used for level-order traversal in trees. | Used for pre-order, in-order, and post-order traversal in trees. |
| Backtracking | No backtracking. | Uses backtracking to explore new branches. |
| Best for | Finding the shortest path in an unweighted graph. | Exploring all possible paths or solving puzzles like mazes. |
| Applications | BFS is used in various applications such as bipartite graphs, shortest paths, etc. If weight of every edge is same, then BFS gives shortest pat from source to every other vertex. | DFS is used in various applications such as acyclic graphs and finding strongly connected components etc. There are many applications where both BFS and DFS can be used like Topological Sorting, Cycle Detection, etc. |
That's all, guys. I hope this article is helpful for you.
Happy Learning... 😀
feedback@javabytechie.com