Red Black Tree vs AVL Tree

   Last Updated: 06 October, 2024       🕓  6 Mins Read

Red Black Tree and AVL Tree are self-balancing tree in Data structure. Both trees maintain their balance through different algorithms, ensuring efficient operations like insertion, deletion, and searching.

In this article, we will learn the basic properties of the Red-black trees and AVL trees and the difference between them.

Introduction to Red-Black Tree

A Red-Black tree is a type of self-balancing binary search tree in which every node is colored either RED or BLACK. The properties of a Red-Black tree decide the color of a node.

In the Red-black tree, every node contains an extra bit that represents a color to ensure that the tree is balanced during any operations performed on the tree, like insertion, deletion, etc.

The Red-Black Tree is introduced by Rudolf Bayer in the year 1972.

Properties of Red Black Tree:

• Red-Black Tree always be a Binary Search Tree (BST).

• Each node in a Red-Black tree will be either RED or BLACK in color.

• The ROOT node must be colored BLACK.

• All the child nodes of RED colored node must be colored BLACK. (Two consecutive RED nodes not possible in the tree).

• There should be the same number of BLACK colored nodes in all the paths of the tree.

• Every leaf node (also called NULL or NIL node) must be colored BLACK.

Example of a Red-Black Tree

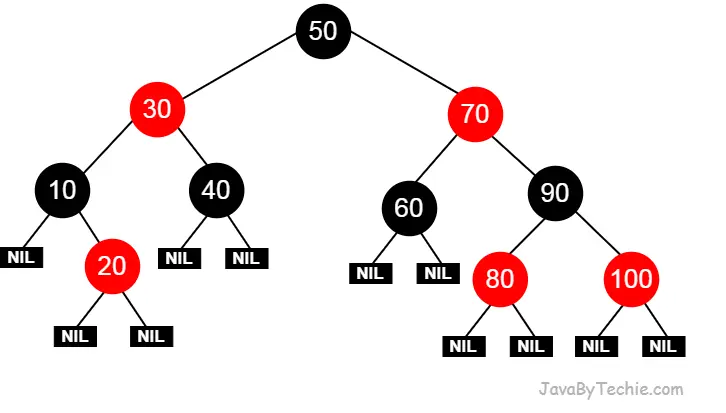
In the given tree above, all the nodes are satisfying all the properties of a Red-Black Tree.

Introduction to AVL Tree

AVL tree is a height-balanced binary search tree. A binary tree is said to be balanced if, the difference between the heights of left and right subtrees of every node in the tree is either -1, 0 or +1. In an AVL tree, every node maintains an extra information known as balance factor.

The AVL tree was introduced in the year 1962 by G.M. Adelson-Velsky and E.M. Landis.

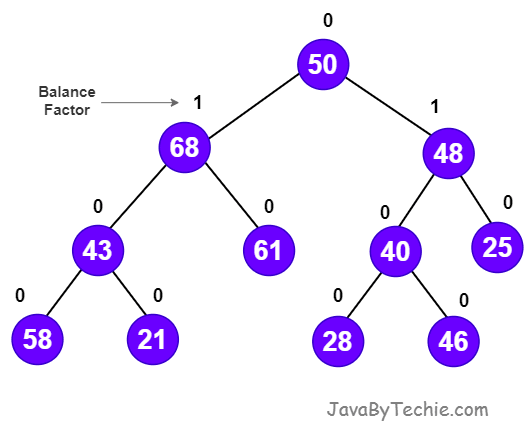
An AVL tree is a balanced binary search tree. In an AVL tree, balance factor of every node is either -1, 0 or +1.

Balance factor of a node is the difference between the heights of the left and right subtrees of that node. The balance factor of a node is calculated either height of left subtree - height of right subtree (OR) height of right subtree - height of left subtree.

Balance factor = heightOfLeftSubtree - heightOfRightSubtree

Difference between Red-Black Tree and AVL Tree

In data structure, the Red-Black Tree and the AVL Tree are both balanced trees, but compared to the red-black tree, the AVL tree is more balanced.

There are many key differences between both the trees as given in the below table.

Red-Black Tree	AVL Tree
Less balanced compared to an AVL tree.	More balanced compared to a Red-Black Tree.
The search operation is less efficient as compared to the AVL tree.	As an AVL tree is strictly balanced, it provides efficient search operations.
Red-Black tree provides faster insertion and deletion operations because it requires fewer rotations to balance the tree.	As AVL trees require multiple rotations to balance the tree, insertion and deletion are slower.
All the nodes must be either red or black in color.	There is no colour for the node.
There is no balance factor for each node.	All the nodes contain a balance factor (-1, 0, 1) so each node takes extra space for storing the balance factor.
To balance the tree, it takes less processing time.	It takes more processing time for processing the tree.