

Last Updated: 06 October, 2024 5 Mins
Graphs are powerful tools for modeling complex relationships and connections between objects and solving real-world problems in various domains. In this tutorial, we have provided a comprehensive explanation of graph data structures, types, representation, traversal, and implementation. Let's begin learning.
A Graph is a non-linear data structure that consists of a set of nodes (also known as vertices) connected by edges (also known as arcs). Each node can represent an object or entity, and each edge represents a connection or link between two nodes.
Graphs are used in the real world to represent various relationships, such as social networks, road networks, electrical circuits, computer networks, and many more.
In general, a graph G is represented as G = ( V , E ), where V is set of vertices and E is set of edges.
To better understanding the above, let's define a basic graph:
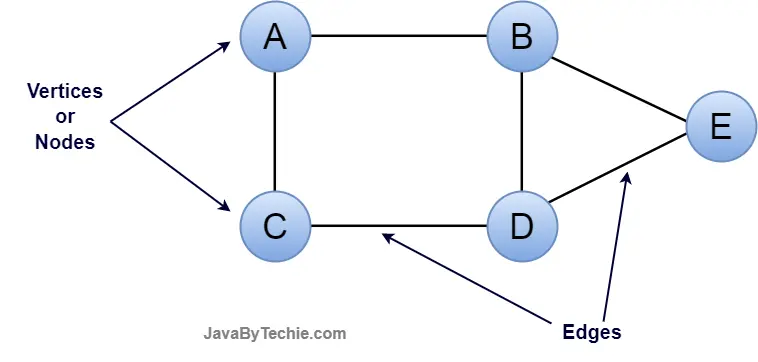
In the given graph above, there are 5 vertices and 6 edges.
This graph G can be defined as G = ( V , E )
Where V = {A, B, C, D, E} and E = {(A,B), (A,C), (B,D), (C,D), (D,E)}.
Vertex: Vertices are the objects or points that join edges. It represents the data. It is denoted by a circle and it must be labeled. There must be one node required to construct a graph.
Edge: An edge is a link that connects two vertices in the graph. It represents the relation between the vertices. Edges are denoted by a line.
Weight: It is labeled to edge. For example, if the distance between two cities is 100 km, then the distance is called weight for the edge.
Path: The path is a way to reach a destination from the initial point in a sequence.
In graph data structure, the process of storing a graph in the memory of a computer is referred to as a graph representation.
A graph in a data structure can be represented in many ways. The two most common ways to represent a graph are:
Adjacency Matrix
An adjacency matrix in a graph is a square matrix used to represent a finite graph. It indicates whether pairs of vertices are adjacent or not in the graph, with rows and columns corresponding to the vertices, and the entries filled with 1s or 0s to signify the presence or absence of edges. Read more...
Adjacency List
An adjacency list in a graph is a collection of lists or arrays that represent the connections between nodes. Each node maintains a list of all the other nodes to which it is directly connected, allowing for efficient traversal and representation of sparse graphs. Read more...
The choice between an adjacency list and an adjacency matrix depends on the specific characteristics of the graph and the operations that will be performed on it.
There are two possible ways to traverse a graph:
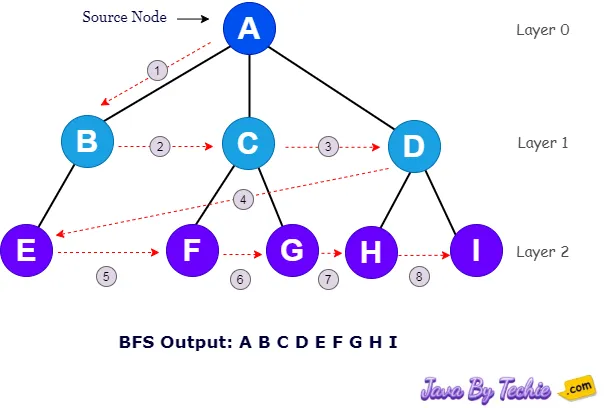
Breadth First Search (BFS): A breadth-first search starts at an arbitrary root vertex and explores all neighboring vertices at the same level before going deeper in the graph.
Depth First Search (DFS): A depth-first search starts at an arbitrary root vertex and explores vertices as deep as possible along each branch before exploring vertices at the same level.
That's all, guys. I hope this article is helpful for you.
Happy Learning... 😀
feedback@javabytechie.com