

Last Updated: 06 October, 2024 5 Mins
A Tree is a hierarchical data structure that consists of nodes connected by edges. Each node contains a value (data) and may have zero or more child nodes. The topmost node in a tree is called the root node, and the nodes at the bottom that do not have children are called leaf nodes.
A tree is a non-linear data structure, meaning that the data is not stored in a sequential order. Trees organize and manage data efficiently and allow easier and quicker searching and sorting the data elements.
Trees organize and manage data efficiently and allow easier and faster searching and sorting of the data elements.
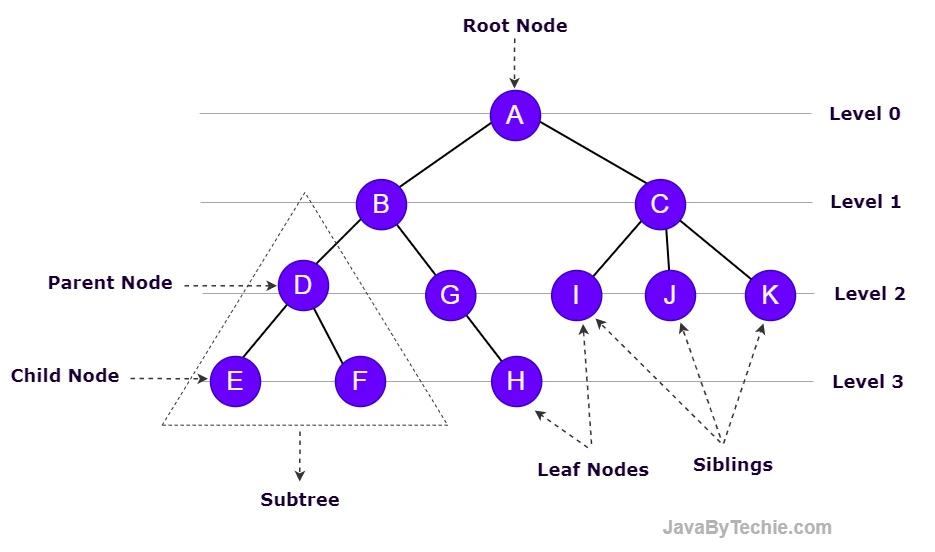
The tree above contains 11 nodes and 10 edges. Keep in mind that a tree with 'N' nodes will have a maximum of 'N-1' edges.
There are the following types of trees in data structure; each is designed in such a way to meet the application requirement.
Let's briefly know about each types of Tree Data Structure.
Binary Tree
A Binary Tree is a special type of tree in which every node can have maximum 2 child nodes. The first part is refered as left child and the second part is right child.
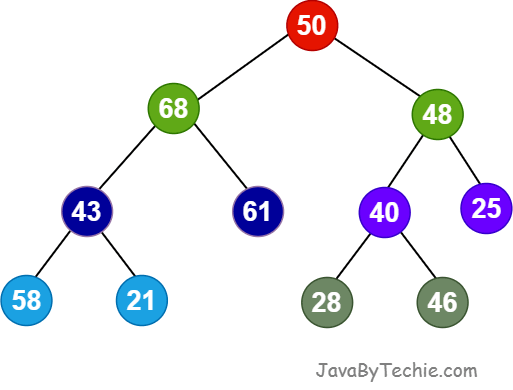
In a Binary Tree, every node has three parts:
Binary Search Tree
A Binary Search Tree (BST) is a special type of data structure that organizes data in a tree-like structure. It has a single starting node called the root, and each node can have at most two child nodes: a left child and a right child.
In BST, the value of each node is greater than all the values in its left subtree and less than all the values in its right subtree. This ordering property makes BSTs efficient for searching, inserting, and deleting elements.
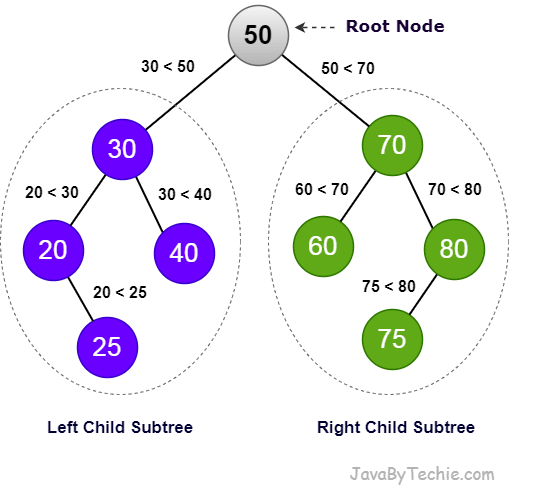
In the tree above, 50 is the Root node and it has two child nodes 30 (create left subtree) and 70 (create right subtree).
Red-Black Tree
A Red-Black tree is a type of self-balancing binary search tree in which every node is colored either RED or BLACK. The color of a node is decided based on the properties of Red-Black tree.
In the Red-black tree, every node contains an extra bit that represents a color to ensure that the tree is balanced during any operations performed on the tree, like insertion, deletion, etc.
Red-Black Tree is introduced by Rudolf Bayer in the year 1972.
Red-Black Tree must be a Binary Search Tree.
Each node in a Red-Black tree will be either red or black color.
The ROOT node must be colored BLACK.
The children of Red colored node must be colored BLACK. (There should not be two consecutive RED nodes).
In all the paths of the tree, there should be same number of BLACK colored nodes.
Every leaf node (also called NULL or NIL node) must be colored BLACK.
AVL Tree
AVL tree is a height-balanced binary search tree. A binary tree is said to be balanced if, the difference between the heights of left and right subtrees of every node in the tree is either -1, 0 or +1. In an AVL tree, every node maintains an extra information known as balance factor.
The AVL tree was introduced in the year 1962 by G.M. Adelson-Velsky and E.M. Landis.
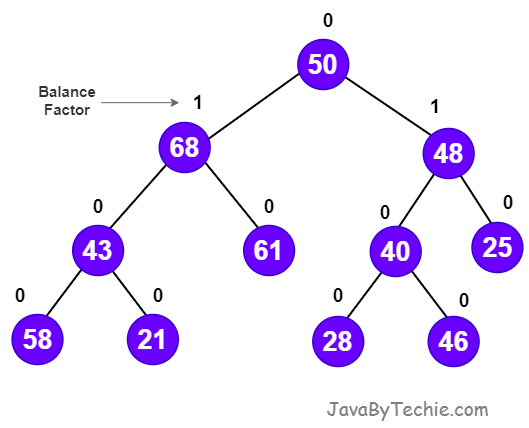
An AVL tree is a balanced binary search tree. In an AVL tree, balance factor of every node is either -1, 0 or +1.
Balance factor of a node is the difference between the heights of the left and right subtrees of that node. The balance factor of a node is calculated either height of left subtree - height of right subtree (OR) height of right subtree - height of left subtree.
Balance factor = heightOfLeftSubtree - heightOfRightSubtree
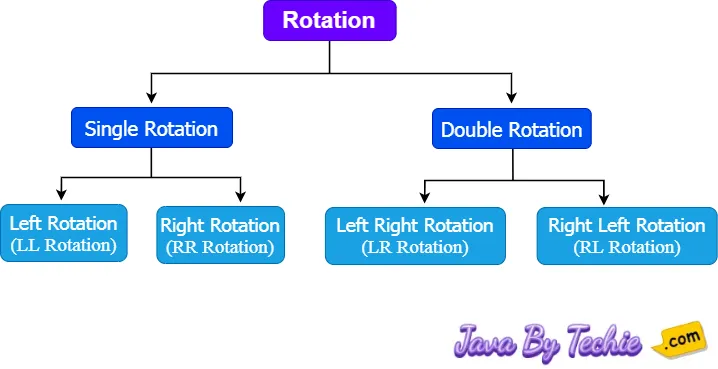
B Tree
In search trees like binary search trees, AVL trees, red-black trees, etc., every node contains only one value (key) and a maximum of two children. However, the B-Tree, a special type of search tree, allows a node to contain more than one value (key) and more than two children, which allows for efficient searching, insertion and deletion of records.
B-Tree can be defined as follows...
B-Tree is a self-balanced search tree in which every node contains multiple keys and has more than two children.
Here, the number of keys in a node and number of children for a node depends on the order of B-Tree. Every B-Tree has an order.
B-tree was invented by Rudolf Bayer and Edward M. McCreight while working at Boeing Research Labs for the purpose of efficiently managing index pages for large random-access files.
Balanced: All leaf nodes are at the same depth, ensuring balance and efficient access times.
Multi-level Nodes: Unlike binary trees, where each node has at most two children, a B-tree node can have multiple children (determined by a parameter called the order of the B-tree).
Variable Node Size: Nodes can hold more than one key (data value), which reduces the height of the tree and thus the number of I/O operations in a database or file system.
Efficient I/O: B-trees are optimized for systems that read and write large blocks of data, such as databases, because they minimize disk I/O by grouping several keys and child pointers in each node.
Insertion and Deletion: These operations are performed in a way that keeps the tree balanced, with reorganization (splitting or merging nodes) done when necessary.
B+ Tree
A B+ Tree is another version of the B tree data structure that allows for efficient insertion, deletion, store, and search operations. In the B+ Tree, all the values (data) are stored in the leaf nodes, and the internal nodes are used only for indexing (like a table of contents).
All the leaf nodes of a B+ Tree are linked together, which provides find a range of values quickly.
Insert: Insert an element into a tree.
Delete: Delete an element from a tree.
Search: Search an element in a tree.
Traversal:
That's all, guys. I hope this article is helpful for you.
Happy Learning... 😀
feedback@javabytechie.com