

Last Updated: 06 October, 2024 5 Mins Read
Graph and Tree are very popular and fundamental Data Structure used in computer science that solve real-world problems in various domains. Both the data structures consist of nodes and edges, a tree is a special type of graph that is acyclic and has a hierarchical structure, whereas a graph can contain cycles and may not have a specific hierarchy.
In this tutoral, we are going to learn about what are Graph and Tree data structure and how both are difference to each other.
A graph is a non-linear data structure that consists of a set of nodes (also known as vertices) connected by edges (also known as arcs). Each node can represent an object or entity, and each edge represents a connection or link between two nodes.
Graph is a powerful and versatile data structure for representing and analyzing complex relationships between objects or entities. In the real world, Graph is used to represent various relationships, such as social networks, road networks, electrical circuits, computer networks, etc.
Generally, a graph G is represented as G = ( V , E ), where V is set of vertices and E is set of edges.
To better understanding the above, let's define a basic graph:
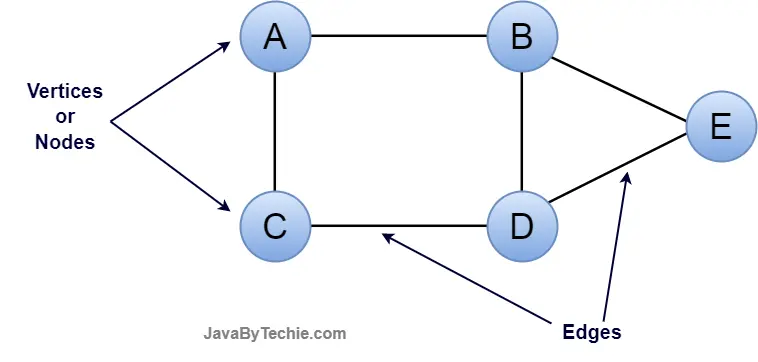
In the given graph, there are 5 vertices and 6 edges.
This graph G can be defined as G = ( V , E )
Where V = {A, B, C, D, E} and E = {(A,B), (A,C), (B,D), (C,D), (D,E)}.
Vertex: Vertices are also know as nodes, vertices are the point that joints edges. It represents the data. It is denoted by a circle and it must be labeled. There must be one node is required to construct a graph.
Edge: An edge is a line that connects two vertices. It represents the relation between the vertices. Edges are denoted by a line. For example, a path to the bus stop from your house.
Weight: It is labeled to edge. For example, the distance between two cities is 100 km, then the distance is called weight for the edge.
Path: The path is a way to reach a destination from the initial point in a sequence.
A tree is a hierarchical data structure that consists of nodes connected by edges. Each node contains a value and may have zero or more child nodes. The topmost node is called the root node, and the nodes at the bottom are called leaf nodes.
A tree is a non-linear data structure, meaning that the data is not stored in a sequential order. Trees are useful for representing hierarchical relationships between data, such as file systems, organizational charts, and family trees.
The Tree data structure allows easier and quicker access to the data element.
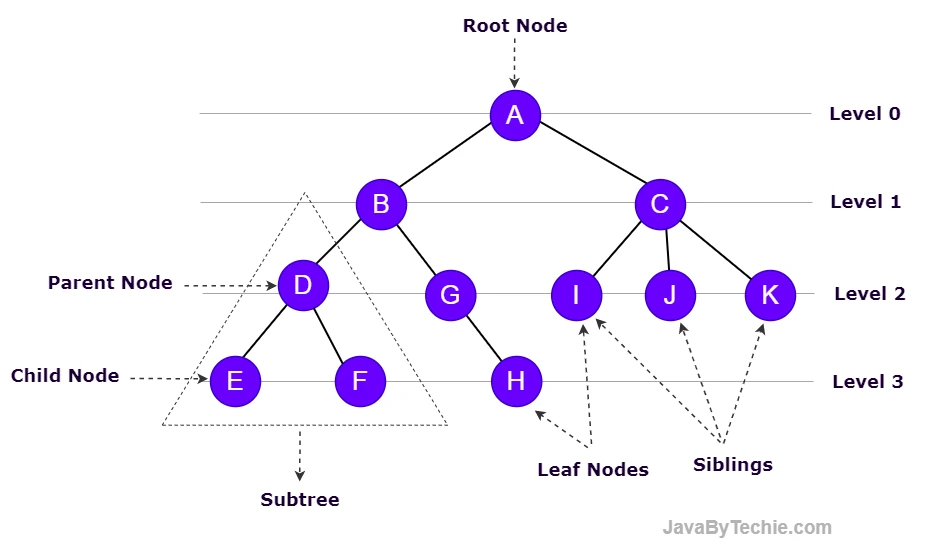
Node: Node is an entity that contains keys and pointer (reference) to its child.
Edge: An edge refers to the link from parent to child. All nodes in a tree connected by edges.
Root Node: A Root Node is a first node or top most node of the tree. Every tree must have a root node and root node does not have a parent node. There will be only one root in a tree.
Parent Node: In a tree data structure, the node that is a node's predecessor is called a Parent node. A parent node has a branch from it to any other node.
Child Node: In a tree data structure, the descendant node of any node is called a child node.
Sibling: Children of the same parent node are called siblings.
Leaf Node: A node which does not have any child node is called a leaf node. A leaf node is the bottom-most node of the tree as we can see in the above image of tree here H, I, G, K are the leaf node the tree. A leaf node is also know as external node.
Ancestor of a Node: Any predecessor nodes on the path of the root to that node are called Ancestors of that node.
Descendant: A node x is a descendant of another node y if and only if y is an ancestor of x.
Level of a node: In a tree data structure, the root node is said to be at level 0, and the children of the root node at level 1 and, the children of the nodes at level 1, will be at level 2.
Internal node: A node has atleast one child node known as an internal.
Neighbour of a Node:Parent or child nodes of that node are called neighbors of that node.
Subtree: In a tree data structure, the sequence of Nodes and Edges from one node to another node is called as PATH between that two Nodes. Length of a Path is total number of nodes in that path.
There are the following major differences between Graph and Queue in the data structure.
| Feature | Graph | Tree |
|---|---|---|
| Definition | A graph is a non-linear data structure that consists of a set of nodes (or vertices) connected by edges (or arcs). Each node can represent an object or entity, and each edge represents a connection or link between two nodes. | A tree is a hierarchical data structure that consists of nodes connected by edges. Each node contains a value and may have zero or more child nodes. |
| Structure | Can have cycles (loops) and disconnected components. | No cycles; connected structure with exactly one path between any two nodes. |
| Root Node | There is no root node in Graph; nodes may have multiple parents or no parents at all. | In the Tree, a top most node is called root node. Every tree must have a root node and root node does not have parent node. |
| Node Relationship | Relationships between nodes are arbitrary. | Tree nodes maintain parent-child relationship; except the root, each node has exactly one parent. |
| Edges | Each node can have any number of edges. | If there is n nodes then there would be n-1 number of edges |
| Traversal Complexity | Traversal can be complicated because of cycles and disconnected components. | Traversal is simple and can be carried out in linear time. |
| Application | Used in many different kinds of scenarios, including social networks, mapping, network optimization, and more. | File systems, organizational charts, HTML DOM, XML documents, and other hierarchical data representations are all commonly used. |
| Examples | Social networks, road networks, computer networks. | File systems, family trees, HTML DOM structure. |
That's all, guys. I hope this article is helpful for you.
Happy Learning... 😀
feedback@javabytechie.com